Identifying Outliers in a Dataset: Techniques using Python, SQL, and Excel
Learn the various techniques used for detecting outliers using popular tools such as Python, SQL, and Excel in this article.
In the realm of data analysis and statistics, identifying outliers is a crucial step to ensure the integrity and quality of your dataset. Outliers, or data points that significantly deviate from the norm, can skew results, impact model performance, and lead to erroneous conclusions.
In this comprehensive guide, we will explore various techniques for detecting outliers using popular tools such as Python, SQL, and Excel, offering insights into each method’s strengths and limitations.
Click HERE for the Dataset used to explain these techniques.
Understanding Outliers
Outliers are data points that deviate significantly from the general pattern or trend of a dataset. They are values that lie far away from the central tendency of the data distribution and can potentially distort the results of data analysis. Outliers can arise due to various reasons, such as measurement errors, data entry mistakes, or genuine extreme observations.
Types of Outliers: Univariate and Multivariate Outliers:
1. Univariate Outliers: Extreme data points in a single variable, detected using methods like z-score or IQR, based on the variable’s distribution. e.g., data significantly deviating from the mean by the threshold of standard deviations.
2. Multivariate Outliers: Extremes in multiple variables together, not necessarily outliers in individual variables. Detected through scattered plots, Mahalanobis distance, or PCA to assess variable relationships.
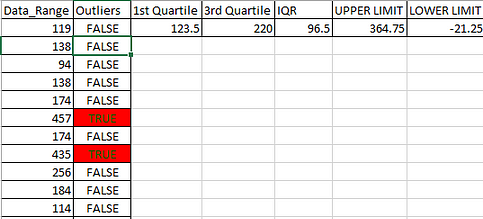
Detecting Outliers in Excel Using IQR (Interquartile Range)
The Interquartile Range (IQR) is a statistical measure that helps identify potential outliers in a dataset by focusing on the spread of the middle 50% of the data.
Here’s how you can use IQR to detect outliers in Excel:
Step One: Organize Your Data
Ensure your data is organized in a column in an Excel spreadsheet.
Step Two: Identify the 1st Quartile of the data range
To find the first quartile of your dataset, input the following formula:
=QUARTILE(data_range, 1)Replace “data_range” with the specific range of your data. The “1” in the formula designates the calculation of the first quartile.
Step Three: Identify the 3rd Quartile of the data range
To determine the third quartile within your dataset, employ this formula:
=QUARTILE(data_range, 3)Substitute “data_range” with the precise range of your data. The “3” in the formula designates the computation of the third quartile.
Step Four: Identify the data range inner quartile (IQR)
Compute the interquartile range (IQR) of your data range using this equation:
=QUARTILE(data_range, 3) - QUARTILE(data_range, 1)Replace “data_range” with the specific range of your data. The IQR signifies the range encompassing the middle 50% of the data.
Step Five: Identify the Upper Limit of the data range
Determine the upper limit of your data range with this formula:
=QUARTILE(data_range, 3) + (1.5 * (QUARTILE(data_range, 3) - QUARTILE(data_range, 1)))Substitute “data_range” with the specific range of your data. This calculation yields the upper boundary for potential outliers.
Step Six: Identify the Lower Limit of the data range
Find the lower limits of your data range using this formula:
=QUARTILE(data_range, 1) - (1.5 * (QUARTILE(data_range, 3) - QUARTILE(data_range, 1)))Replace “data_range” with the specific range of your data. This computation establishes a lower threshold for potential outliers.
Step Seven: Check for outliers in the data range using the =OR function
To identify outliers in the data range, utilize the `=OR` function as follows:
=OR(data_value > UpperLimit, data_value < LowerLimit)In this formula, replace “data_value” with the actual cell reference (e.g., B2) that contains your data point. If the value in B2 is greater than the Upper Limit, it’s flagged as an outlier. Similarly, if the value in B2 is less than the Lower Limit, it’s also flagged as an outlier.
Step Eight: Highlight Outliers
Use conditional formatting to highlight data points that fall outside the defined threshold. You can use the IF function combined with logical conditions to achieve this.
Detecting Outliers in SQL Using Z-score
Detecting outliers in SQL using the Z-score involves computing the Z-score for each data point in a given column and then identifying those that fall beyond a specified threshold.
Here’s how you can do it:
Step One: Explore the dataset
Conduct an exploratory analysis of the dataset to gain insights into the data values and columns that will be the focus of your work.
-- Explore the data
SELECT *
FROM outliers_with_sql;Step Two: Calculate the Mean and Standard Deviation of the Data.
-- Calculate the mean and standard deviation of the Data.
SELECT
AVG(order_qty) AS mean_value,
STD(order_qty) AS std_deviation
FROM
outliers_with_sql;Utilize SQL aggregate functions such as AVG() and STDEV() to compute the mean and standard deviation of the data under examination.
Step Three: Calculate the Z-Score for Each Data Point
Subsequently, calculate the z-score for each individual data point using the formula:
z = (value — mean) / standard_deviation.
-- Calculate the Z-Score for Each order_qty Data Point
SELECT
order_ID,
order_qty,
AVG(order_qty) over () AS mean_value,
STD(order_qty) over () AS std_deviation,
(order_qty - AVG(order_qty) over() ) / STD(order_qty) over() AS z_score
FROM
outliers_with_sql,
(SELECT AVG(order_qty) AS mean, STD(order_qty)
AS standard_deviation FROM outliers_with_sql) AS stats;Incorporate the window function within your query to allow for the visualization of the z-scores for each data point, if applicable.
Step Four: Identifying Outliers with a Threshold Value of 1.5
-- Identifing Outliers with Threshold value of 1.5
SELECT *
FROM (SELECT
order_ID,
order_qty,
(order_qty - AVG(order_qty) over() ) / STD(order_qty) over() AS z_score
FROM
outliers_with_sql,
(SELECT AVG(order_qty) AS mean, STD(order_qty)
AS standard_deviation FROM outliers_with_sql) AS stats) as outliers
WHERE z_score > 1.5 OR z_score < -1.5Once z-scores have been calculated, you can establish a threshold value (e.g., 1.5) to designate data points as outliers. Any values with z-scores surpassing the threshold, whether positive or negative, are indicative of potential outliers.
Detecting Outliers in Python Using IQR (Interquartile Range)
Detecting outliers in Python using the Interquartile Range (IQR) involves utilizing the statistical measure of IQR to identify potential outliers in a dataset.
Quick Reminder on IQR Method of Outliers Detection The Interquartile Range (IQR) method is a statistical technique used to detect and handle outliers in a dataset. The IQR represents the range between the first quartile (Q1) and the third quartile (Q3) of a dataset.
Here’s how you can do it:
Step One: Load and Generate Data
Start by loading your dataset into Python using libraries like Pandas or Numpy, or you can generate sample data for demonstration.
# Loading libraries acsv file
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv(r"xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx.csv")
df.headBefore we proceed to the second step, let’s use the boxplot in Python to identify our outliers.
# Using boxplot to see the outliers clearly
df.boxplot()As evident from the visual above, our dataset includes outlier data values, and the following approach will be employed to detect and identify these values.
Step Two: Identifying the 1st quartile
To find the first quartile (q1), we compute the value at the 25th percentile, which corresponds to the ‘order_qty’ column. This is achieved by utilizing the `.quantile()` function with a parameter of 0.25.
# Identifying the 1st quartile
q1 = df['order_qty'].quantile(0.25)
print(q1)Step Three: Identifying the 3rd quartile
The calculation for q3 involves determining the value at the 75th percentile (third quartile) of the ‘order_qty’ column using the `.quantile()` function with a parameter value of 0.75.
# Identifying the 3rd quartile
q3 = df['order_qty'].quantile(0.75)
print(q3)Step Four: Calculating IQR (Inter Quartile Range)
Calculating the interquartile range (IQR) involves finding the difference between q3 and q1, which signifies the range between the first and third quartiles.
# Calculating the Inter Quartile Range Method
iqr = q3-q1
print(iqr)Step Five: Calculate the upper & lower limit using the IQR
To determine the upper limit, we add 1.5 times the IQR to Q3 (q3 + 1.5 * IQR). Conversely, the lower limit is obtained by subtracting 1.5 times the IQR from Q1 (q1–1.5 * IQR).
# Calculate the upper and lower limit using the IQR
upper_limit = q3 + (1.5 * iqr)
lower_limit = q1 - (1.5 * iqr)
print(lower_limit, upper_limit)Step Six: Detecting the IQR using Boolean Indexing
Boolean indexing is employed to filter the DataFrame, selecting rows where the ‘order_qty’ values fall beyond the computed limits (Upper and Lower Limits).
# Detecting the Outliers
df.loc[(df['order_qty'] > upper_limit) | (df['order_qty'] < lower_limit)]Your support is invaluable
Did you like this article? Then please leave a share or even a comment, it would mean the world to me!
Don’t forget to subscribe to my YouTube account HERE, Where you will get a video explaining this article!















Great write up